
West, D.B.: Introduction to Graph Theory, 2nd edn. Shannon, R.W.: Simplicial cells in arrangements of hyperplanes. Klivans, C., Swartz, E.: Projection volumes of hyperplane arrangements. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. Algebres de dimension infinie, groupes des tresses et groupes. Cambridge University Press, Cambridge (1990) In geometry, a hyperplane is a subspace whose dimension is one less than that of its ambient space. On two-dimensional homology classes of four- manifolds, Math. In two dimensions, we can picture the hyperplane as a straight line. When two convex sets do not intersect, it is possible to find a hyperplane that separates them. This property can be used to prove convexity for a wide variety of situations. Humphreys, J.: Reflection Groups and Coxeter Groups, Cambridge Studies in advanced mathematics, vol. The intersection of a (possibly infinite) family of convex sets is convex. Le premier sera l’ensemble d’apprentissage, et le deuxième sera l’ensemble de test. Si un espace est en 3 dimensions alors ses hyperplans sont. En géométrie, un hyperplan est un sous-espace dont la dimension est inférieure dune unité à celle de son espace ambiant. Un plan est un hyperplan de dimension 2, lorsquil est noyé dans un espace de dimension 3.

Grove, L.C., Benson, C.T.: Finite Reflection Groups, Graduate Texts in Mathematics, vol. Deux plans sécants dans l espace tridimensionnel.
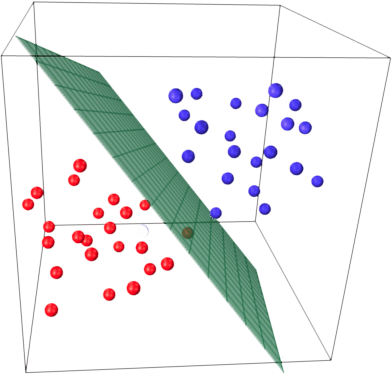
Princeton University Press, Princeton (2008)ĭrton, M., Klivans, C.: A geometric interpretation of the characteristic polynomial of reflection arrangements. bound, we can only assert that the probability of some hyperplane having a large margin is at most the probability of any one having a large margin times the number of hyperplanes (which is infinite). Cambridge University Press, Cambridge (1999)ĭavis, M.: The Geometry and Topology of Coxeter Groups, London Mathematical Society Monographs Series, 32. Encyclopedia of Mathematics and its Applications, 46. Springer, New York (2005)ījörner, A., Las Vegas, M., Sturmfels, B., White, N., Ziegler, G.: Oriented Matroids, 2nd edn. Thus, parallel hyperplanes, which did not meet in the affine space, intersect in the projective completion due to the addition of the hyperplane at infinity.Björner, A., Brenti, F.: Combinatorics of Coxeter Groups, Graduate Texts in Mathematics, vol. This is the option that is more often used.
So, another possibility is to say that a hyperplane is the zero set of a linear functional. InfinitePlane can be used as a geometric region and graphics primitive. In the projective space, each projective subspace of dimension k intersects the ideal hyperplane in a projective subspace "at infinity" whose dimension is k − 1.Ī pair of non- parallel affine hyperplanes intersect at an affine subspace of dimension n − 2, but a parallel pair of affine hyperplanes intersect at a projective subspace of the ideal hyperplane (the intersection lies on the ideal hyperplane). For finite dimension a hyperplane is the zero set of a linear form (a linear functional), a linear function from the space to the scalar field. InfinitePlane is also known as plane or hyperplane. The resulting projective subspaces are often called affine subspaces of the projective space P, as opposed to the infinite or ideal subspaces, which are the subspaces of the hyperplane at infinity (however, they are projective spaces, not affine spaces).
Each affine subspace S of A is completed to a projective subspace of P by adding to S all the ideal points corresponding to the directions of the lines contained in S. Adjoining the points of this hyperplane (called ideal points) to A converts it into an n-dimensional projective space, such as the real projective space RP n.īy adding these ideal points, the entire affine space A is completed to a projective space P, which may be called the projective completion of A. The union over all classes of parallels constitute the points of the hyperplane at infinity. Similarly, starting from an affine space A, every class of parallel lines can be associated with a point at infinity.


 0 kommentar(er)
0 kommentar(er)
